오일러 각
짐벌락 현상은 오일러 각을 사용할 떄 발생하는 문제 현상입니다.
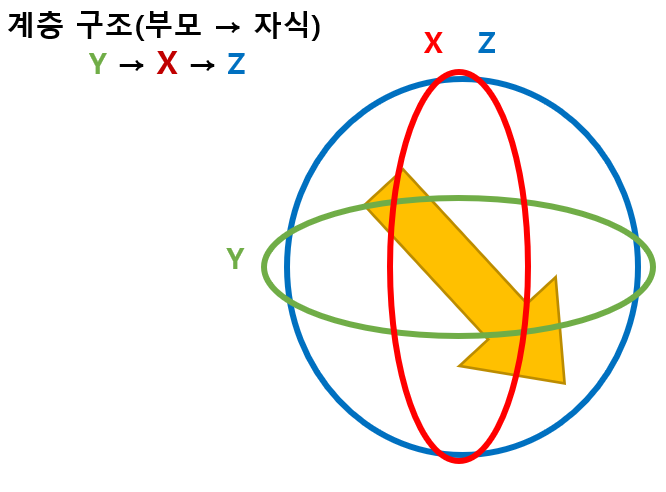
위의 사진은 Y가 부모인 오일러 각을 그림으로 나타낸 것입니다.
계층 구조상 Y축이 회전하면 모든 축이 회전합니다. 반대로 Z축은 혼자서만 회전합니다. X축은 회전할 때 Z축에 영향을 줍니다. 만약 이상태에서 Z축을 회전시킨다고 했을 때 상황은 아래처럼 됩니다.

X축을 회전시켰을 뿐인데 Z축이 X축의 자식이므로 Y축과 Z축이 겹치게 됩니다. 이 상태에서 화살표를 아래방향으로 하려고 할 때 돌릴 수 있는 축이 없어지기 때문에 문제가 발생합니다. 사라진 축을 점선으로 표시했습니다. 이렇게 3차원 공간에서 2개의 축이 겹칠 때를 짐벌락 상태라고 합니다. 짐벌락은 오일러 각을 사용하는 이상 어떻게 하던간에 발생합니다.
짐벌락을 최소화 할 수 있는 방법은 가장 자주쓰이는 축을 부모로 두고 가장 적게 쓰는 축을 그 자식으로, 남은 축을 그 자식으로 넣는 방법입니다.
오일러 각이 두 축의 회전에 대해서 보간이 성립하지 않는 이유
오일러 각이 두 축의 회전에 대해 보간이 성립하지 않는 이유는 처음 부터 (30도, 40도, 50도)회전한 결과와 (20도, 30도, 40도)씩 회전 한 후(10도, 10도, 10도)를 더 회전한 결과가 다르기 때문입니다.
수학공식으로 설명하겠습니다.
(R_yaw * R_pitch * R_roll)
(R_yaw20 * R_pitch30 * R_roll40) * (R_yaw10 * R_pitch10 * R_roll10)
= R_yaw20 * R_pitch30 * R_roll40 * R_yaw10 * R_pitch10 * R_roll10
공식으로 썼을 때 위의 식처럼 나오게 되면서 (30도,40도,50도)를 회전한 값과 같다고 볼 수 없게 됩니다.
보간은 덧셈이 성립했을 때 가능함으로 오일러 각은 두 축의 회전에 대해서 보간이 성립하지 못합니다.
만약 식이 아래처럼 나오면 보간이 가능합니다.
(R_yaw20 * R_yaw10) * (R_pitch30 * R_pitch10) * (R_roll40 * R_roll10)
로드리게스 회전공식
로드리게스 회전은 3차원상의 물체의 회전을 회전축과 그 각도로 설명합니다.
아래 그림은 벡터 p가 회전축 n에 대해 세타만큼 회전한 벡터p'를 수식으로 나타낸 것입니다.

평면의 방정식
평면을 이루는 최소한의 요소로는 노멀벡터 하나와 점 하나가 필요합니다.
P(x, y, z)와 P'(x, y, z) 그리고 크기가 1인 노멀벡터 n(a, b, c)가 있다고 할 때 평면의 방정식을 그림으로 나타내 보겠습니다.

P' - P벡터는 노멀벡터 n과 직교합니다. 그 뜻은 두 벡터의 내적값이 0이 됩니다. 수식으로 나타내 보겠습니다.
n dot (P - P') = (a, b, c)(x - x', y - y', z - z') = 0
a(x - x') + b(y - y') + c(z - z') = 0
ax + by + cz - (ax' + by' + cz') = 0
ax + by + cz +d = 0이 되므로 즉 d = -(ax' + by' + cz')가 됩니다.
여기서 P' dot n = (ax' + by' + cz')이므로
d = -P' dot n이 됩니다.
이 때 d가 가지는 의미는 원점으로부터의 거리에 -를 붙인 값이 됩니다.
d의 값이 양수면 평면의 방향이 원점을 향하고, 음수면 면의 방향이 원점에서 멀어진다는 뜻입니다.
프러스텀
뷰좌표계를 기준으로 프러스텀을 이루는 평면의 방정식을 나타내 보겠습니다.
저번 포스팅에서 썼던 그림을 가져와 보겠습니다.

이 때 Near의 값은 10, Far의 값은 1000이라고 가정하겠습니다.
여기서 근평면의 평면의 방정식은
(0, 0, -10)
Normal : (0, 0, 1)
d의 값 : -10
z + 10 = 0
원평면의 평면의 방정식은
Normal : (0, 0, -1)
d의 값 : -1000 (원점으로부터 멀어지기 때문에)
-z - 1000 = 0
다음으로 근평면과 원평면 사이의 빨간 원 부분의 평면의 방정식을 구해보겠습니다.
d의 값 : 0(원점을 지나기 때문에)
여기서 시야각을 세타라고 할 때 세타/2만큼 회전한 것이 되기 때문에P' = (0, sin(세타/2), cos(세타/2))N = (0, cos(세타/2), -sin(세타/2))가 나오게 됩니다.
평면의 방정식은
cos(세타/2)y - sin(세타/2)z = 0이 됩니다.
같은 방식으로 다른 평면도 구할 수 있습니다.
'엔진프로그래밍' 카테고리의 다른 글
| 한 학기 동안 정리한 것들 (0) | 2020.07.19 |
|---|---|
| 투영 보정 매핑 (0) | 2020.07.19 |
| 백페이스 컬링과 원근 투영 (0) | 2020.07.08 |
| 회전 행렬과 LookAt 행렬 (0) | 2020.07.01 |
| UV좌표와 뷰 좌표계 (0) | 2020.06.24 |



