투영 보정 매핑

이전에 원근투영에 대하여 설명했었습니다. 그 때 3D 큐브를 선으로 나타내어 보았지만 사실 그대로 사용하면 문제가 발생합니다. 문제는 텍스쳐를 매핑할 때 나타납니다.

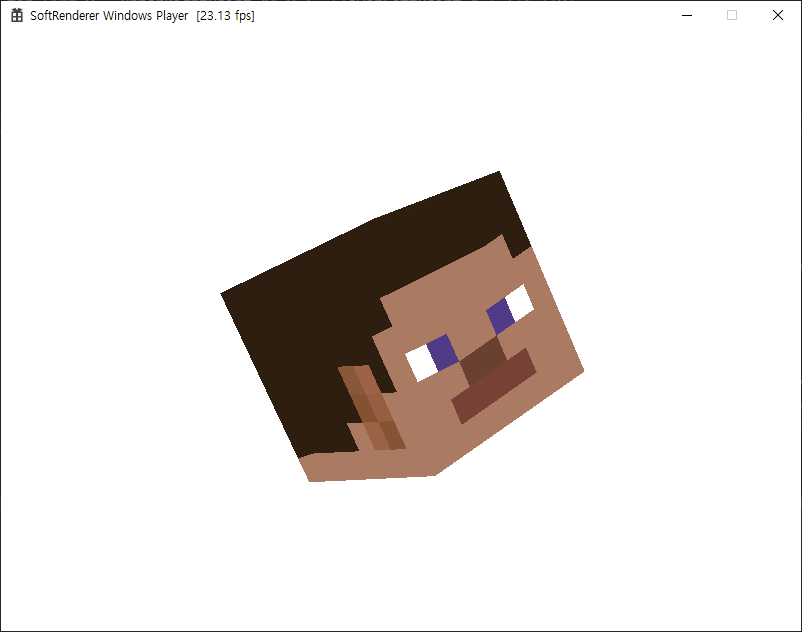
텍스쳐를 매핑하면 살짝 화가난 것 처럼보이는 스티브를 볼 수 있습니다.

이렇게 나오는 이유는 위 사진에서 보이듯이 p의 무게 중심 좌표는 0.5입니다.

하지만 v의 무게 중심 좌표는 0.5가 아닙니다. 그래서 위의 스티브의 얼굴이 카메라의 각도에 따라 다르게 나타나는 것입니다. 따라서 p의 좌표를 기준으로 v의 무게 중심 좌표를 보간해야 올바른 결과가 나옵니다. 이를 투영 보정 매핑이라고 합니다.

해결 방법

 

현재 우리가 알고 있는 값은 NDC좌표계로 산출된 p의 무게 중심 값$$(1 - s - t, s, t)$$삼각형의 각 점의 NDC좌표와 Clip 좌표계의 Wc 값$$(W_{c} = -view_{z})$$

이 값들을 사용해서 p의 무게 중심 값으로부터 역 추적하여 v를 구해야 합니다.

첫번째로 Clip좌표계에서 NDC좌표계로 넘어갈 때 Wc값을 나눠줘야 합니다. 이 뜻은 NDC좌표계는 Wc에 반비례한다는 을 알 수 있습니다.

위 그래프 처럼 점이 3개가 있다고할 때 이 점들 사이의 중점은(0,1,4)입니다.

점들을 투영하면 다음과 같이 나옵니다.

하지만 투영 후의 보간을 거치면 $(1 - s  - t)$라서 중점 값이 $(0, \frac{1}{3})$로 나오게 됩니다.

이 값은 위에서 구한 값과 다르기 때문에 실제 값을 찾아야 합니다.

 

수식

NDC 좌표 값으로붕터 산출된 비율 값으로 보간된 $z'$를 구하는 방법

$$\frac{1}{z'} = \frac{1}{z_{0}} + q \cdot(\frac{1}{z_{1}}- \frac{1}{z_{0}})$$

뷰 좌표계의 실제 비율$t$의 값으로 이를 구하는 경우

$$z' = z_{0} + t(z_{1} - z_{0})$$

q의 값은 알지만 t의 값은 모르기에 q로부터 t를 구하려면 다음과 같은 수식이 만들어집니다.

$$\frac{1}{z_{0}}+ q \cdot (\frac{1}{z_{1}} - \frac{1}{z0}) = \frac{1}{z_{0}+t(z_{1}-z_{0})}$$

$$t = \frac{q \cdot z_{0}}{q \cdot z_{0} + (1-q) \cdot z_{1}}$$

위 공식을 이용하면 $t$의 값을 구할 수 있습니다.

 

세 점에 대한 무게중심 좌표 $t_{s},t_{t},1-t_{s}-t_{t}$는 아래과 같이 나옵니다.

$$t_{s} = \frac{q_{s} \cdot z_{0}}{q_{s} \cdot z_{0} + q_{t} \cdot z_{1} + (1-q_{s}-q_{t} \cdot z_{2})}$$

$$t_{t} = \frac{q_{t} \cdot z_{1}}{q_{s} \cdot z_{0} + q_{t} \cdot z_{1} + (1-q_{s}-q_{t} \cdot z_{2})}$$

$$1-t_{s}-t_{t} = \frac{(1-q_{s}-q_{t})\cdot z_{2}}{q_{s} \cdot z_{0}+q_{t} \cdot z_{1}+(1-q_{s}-q_{t}) \cdot z_{2}}$$

결과