브레젠험 알고리즘이란?
두 점 (x1, y1), (x2, y2)에 대한 직선의 방정식은 다음과 같습니다.


직선의 방정식으로 완벽한 선을 그리려면 float 자료형으로 표현해야 합니다. 하지만 모니터의 픽셀 좌표는 정수형이기 때문에 int 자료형을 사용하는 브레젠험 알고리즘으로 선을 그릴 수 있습니다.
원리

브레젠험 알고리즘은 현재 픽셀로부터 다음 픽셀을 어떻게 선택할지가 핵심입니다. 기울기가 0과 1사이이므로 x의 값은 항상 1씩 증가합니다. 그렇다면 매번 y의 값을 이전과 같은 값으로 유지할지 또는 1 증가된 값을 선택할지가 핵심입니다.
위 그림에서 왼쪽 아래 픽셀이 초기값이고 오른쪽으로 갈수록 x의 값이 증가한다고 하면, 브레젠험 알고리즘은 그림의 초록색선과 빨간색선 중 값이 더 작은 경우를 찾고 초록색선이 더 짧은 경우 값을 유지하고 빨간색선이 더 짧은 경우 y를 1 증가시킵니다.
1팔분면에 대하여 선 전개하기



이 좌표를 사용하여 판별식을 계산해보면
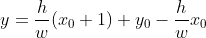

이 상태에서 양변에 w를 곱하면

x0와 y0에 0을 대입하면

여기서 양변에 2를 곱하면


이렇게 판별식이 완성됩니다.
다음으로 두 번째 x위치에 대한 y의 값을 찾아보면,

아까와 같은 방식으로 하면



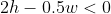


이렇게 나옵니다.
같은 방법으로 두 번째 위치에 대한 판별식은 다음과 같습니다.

이렇게 두가지를 해봄으로써 판별식의 패턴을 찾을 수 있습니다.
처음에는 두 번째 픽셀의 y값을 정하기 위하여 2h-w를 적용합니다.
그 후 판별식을 통해 다음 픽셀의 y값이 그대로 유지되면, 다음 판별식은 2h를 더한 값이 됩니다.
y의 값이 그대로 유지되지않고 한 칸 증가하면, 다음 판별식은 2h-2w를 더한 값이 됩니다.
x값이 목표에 도달할 때까지 계속 반복하면 됩니다.
다른 팔분면에서의 선 전개방법

1팔분면에서는 x를 증가시키고 y의 값을 판별했습니다.
반대로 2팔분면에서는 y를 증가시키고 x의 값을 판별하면 구할 수 있습니다.
2팔분면에서의 판별식

8팔분면은 x가 증가함에따라 y가 줄어들면 선을 전개할 수 있습니다.
나머지 다른 팔분면에서도 같은 방법으로 선을 전개할 수 있습니다.
최종 결과
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
int width = abs(endPosition.X - startPosition.X);
int height = abs(endPosition.Y - startPosition.Y);
// 여기서 부터 구현
SetPixel(startPosition, InColor);
int x = startPosition.X;
int y = startPosition.Y;
int YValue = InEndPos.Y >= 0 ? -1 : 1;
int XValue = InEndPos.X >= 0 ? 1 : -1;
// 1,4,5,8 팔분면일 경우
if (width > height)
{
int det = (2 * height) - width; // 판별식
for (x = startPosition.X; x != endPosition.X; x += XValue)
{
if (det < 0)
{
det += 2 * height;
}
else
{
y += YValue;
det += (2 * height - 2 * width);
}
SetPixel(ScreenPoint(x, y), InColor);
}
}
// 2,3,6,7 팔분면일 경우
else
{
int det = (2 * width) - height; // 판별식
for (y = startPosition.Y; y != endPosition.Y; y += YValue)
{
if (det < 0)
{
det += 2 * width;
}
else
{
x += XValue;
det += (2 * width - 2 * height);
}
SetPixel(ScreenPoint(x, y), InColor);
}
}
|
cs |

'엔진프로그래밍' 카테고리의 다른 글
| 회전 행렬과 LookAt 행렬 (0) | 2020.07.01 |
|---|---|
| UV좌표와 뷰 좌표계 (0) | 2020.06.24 |
| Galois Field와 아핀 조합 (0) | 2020.06.10 |
| 코헨 서덜랜드 알고리즘 구현 (0) | 2020.06.03 |
| 엔진프로그래밍 수학 수업 정리 (0) | 2020.05.31 |



